1. Introduction

In the contemporary industrial technology ecosystem, permanent magnet synchronous motors (PMSM) serve as the core device for power conversion and are widely integrated in high reliability scenarios such as aerospace [1]. However, the performance degradation during low-speed operation exposes potential flaws in the algorithm model [2]. In addition, when the operating parameters of the system exceed the steady-state range preset by the model, the efficiency of the estimation algorithm based on ideal assumptions deteriorates in the robustness dimension, indicating the urgent need to establish a more inclusive control theory framework [3]. The introduction of sliding mode control (SMC) marks a shift in control theory from the asymptotic stability paradigm to the finite time convergence paradigm. However, the technological potential of this control paradigm is still limited by specific constraints at the physical implementation level [4]. The engineering practice of early sliding mode observers has shown that the existence of high-frequency chattering phenomenon reveals a mismatch between theoretical models and physical implementations [5], and the trade-off effect between estimation accuracy and system stability is common [6]. The proposal of high-order sliding mode observer and super spiral sliding mode control [7] can be seen as a progressive correction to this technical paradox.

However, current research mostly focuses on local optimization under specific parameters, lacking comprehensive analysis of the overall system performance under multiple parameter variations [8]. Therefore, how to optimize dynamic response and high-frequency pulsation suppression through robust design of the system remains an unsolved problem in current PMSM sensorless control technology. Based on this, this article proposes an improved sliding mode observer that effectively improves the accuracy under low speed and high load conditions; An in-depth analysis was conducted on the impact of resistance, inductance, and magnetic flux deviation on system performance, revealing that magnetic flux deviation is the core bottleneck of system accuracy; Designed an efficient robustness mechanism to solve the performance degradation problem of traditional control methods under parameter changes.

2. Research design

2.1. Model establishment

Accurate mathematical models are the foundation for designing high-performance sensorless control algorithms. This section establishes its mathematical model in the stationary reference frame of α - β and explicitly expresses the relationship between key electrical variables and rotor position and velocity [9].

The specific process is detailed in Appendix A. The Stator Voltage Equations in α - β Frame are constructed as follows:

$$ \frac{d}{dt}\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]=\mathit{A}\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]+\frac{1}{{\mathit{L}}_{s\left(\alpha \beta \right)}}\left(\left[\begin{array}{c}{v}_{\alpha }\\ v_{\beta }\end{array}\right]-\left[\begin{array}{c}{e}_{\alpha }\\ e_{\beta }\end{array}\right]-R_s\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]\right)+\mathit{\Delta }$$(1)

Among them, A is a term related to inductance and positionl; L_s(αβ) is the equivalent inductance matrix in the αβ coordinate system; Δ represents disturbances not included in the model.

2.2. Observer design

This section designs an improved sliding mode observer structure based on the PMSM mathematical model established in the previous section.

From equation (1):

$$ \frac{d}{dt}\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]=\frac{1}{L_s}\left(\left[\begin{array}{c}{v}_{\alpha }\\ v_{\beta }\end{array}\right]-R_s\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]-\left[\begin{array}{c}{e}_{\alpha }\\ e_{\beta }\end{array}\right]\right)$$(2)

Among them, e_α and e_β are the back electromotive force components that need to be observed.

Design a sliding mode observer as follows:

$$ \frac{d}{dt}\left[\begin{array}{c}{\widehat{i}}_{\alpha }\\ {\widehat{i}}_{\beta }\end{array}\right]=\frac{1}{L_s}\left(\left[\begin{array}{c}{v}_{\alpha }\\ v_{\beta }\end{array}\right]-R_s\left[\begin{array}{c}{\widehat{i}}_{\alpha }\\ {\widehat{i}}_{\beta }\end{array}\right]-\left[\begin{array}{c}{\widehat{e}}_{\alpha }\\ {\widehat{e}}_{\beta }\end{array}\right]-\left[\begin{array}{c}{z}_{\alpha }\\ z_{\beta }\end{array}\right]\right)$$(3)

Among them, î_α, î_β: The stator current components of the α and β axes estimated by the observer; ê_α, ê_β: The initial estimated or set back electromotive force term within the observer; z_α, z_β: Key design term - sliding mode variable structure control term, designed in the form of a switching function, used to drive observation error convergence and approximate the actual back electromotive force.

Choose sliding surface s:

$$ \mathit{s}={\left[\begin{array}{cc}{s}_{\alpha }& s_{\beta }\end{array}\right]}^T={\left[\begin{array}{cc}{\tilde{i}}_{\alpha }& {\tilde{i}}_{\beta }\end{array}\right]}^T=0$$(4)

The physical meaning of the sliding surface is the state plane where the current estimation error is zero. The objective of the observer is to make the system state (î_α, î_β) reach and maintain motion on the sliding surface s=0 within a finite time.

Stability analysis can be found in Appendix B.

2.3. Theoretical analysis of robustness of key motor parameters

Sliding mode control endows the permanent magnet synchronous motor with excellent disturbance rejection capability for the sensorless system [10], but the robustness levels for different parameters are distinct. The system exhibits the strongest inherent tolerance to changes in stator resistance, and an increase in its value actually enhances damping and accelerates convergence in the observer, with little impact on controller speed tracking; The robustness to changes in the inductance of the orthogonal axis is moderate, and the inductance changes mainly affect the transient convergence speed and accuracy of the observer. However, after entering sliding mode motion, the core disturbance can be effectively suppressed, and the dynamic impact on the controller is limited; However, the magnetic flux of permanent magnets is a key bottleneck that determines system accuracy. Its decrease under extreme conditions may threaten the stability of the observer, but theoretically does not affect the correctness of its position and phase estimation. The real core challenge lies in the fact that any deviation between the actual value of the magnetic flux and the preset value of the internal model of the controller will result in an electromagnetic torque model mismatch that cannot be completely eliminated by sliding mode robustness and is proportional to the degree of error. This will inevitably introduce residual systemic steady-state tracking errors in the speed loop, becoming the fundamental bottleneck factor that restricts the maximum accuracy limit of the system. The "matching" robust mechanism of sliding mode can effectively handle resistance, inductance, and conventional disturbances, but it is powerless against the fixed magnetic flux parameter errors in the controller model.

3. Simulation and experimental verification

3.1. Parameter settings

The key parameters related to PMSM experiments can be found in Appendix C.

3.2. Dynamic performance testing

This section focuses on the dynamic performance differences of the sliding mode control sensorless scheme (SMO+SMC) compared to the benchmark method (PI observer+PI controller) [11]. The key observation indicators for dynamic performance testing include low-speed steady-state position estimation error RMS, speed step adjustment time, speed step overshoot, load jump recovery time, and steady-state position estimation error (mean). The specific results are shown in Table 1.

This scheme demonstrates significant and reliable performance advantages in low-speed observation accuracy (-50%), dynamic response speed (-28%), suppression of system overshoot (-56%), enhancement of load mutation recovery capability (-33%), and reduction of steady-state position estimation bias.

Among them, the specific situation of the position estimation error in this article's scheme is shown in Figure 1. The temporal data of position error indicates that the system has achieved high-precision and low-noise position estimation. This meets the stringent requirements of industrial grade servo drives for position observation accuracy, providing a feasible engineering solution for high-speed and high-precision sensorless control.

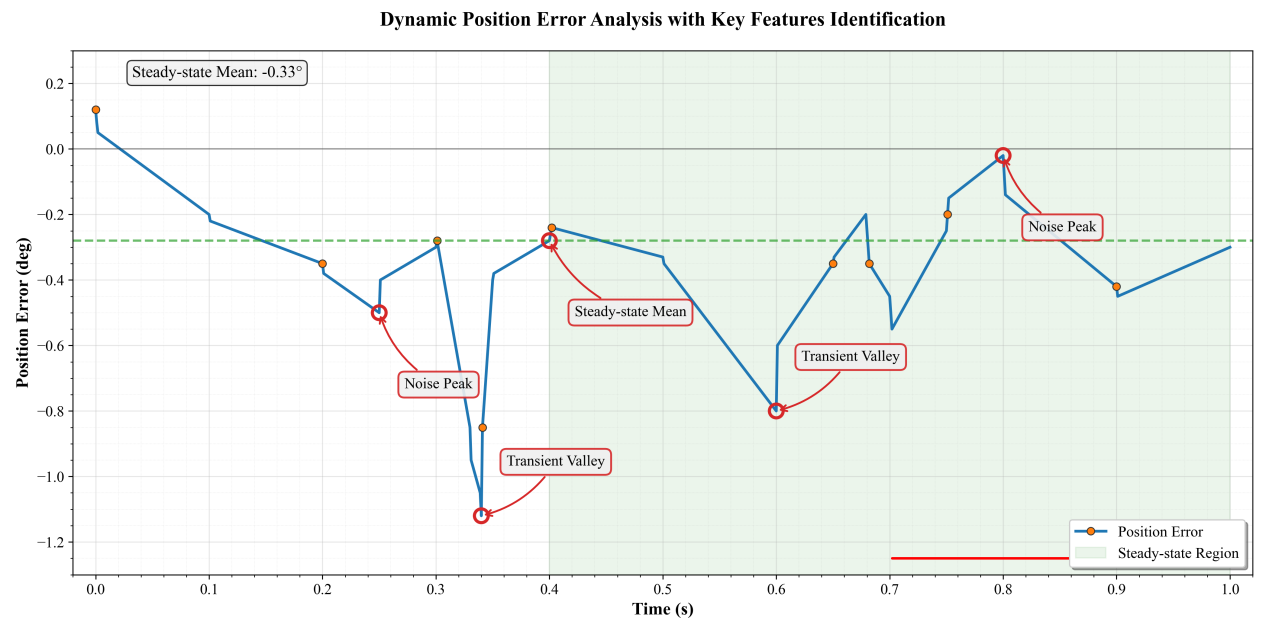
3.3. Parameter robustness analysis experiment

To rigorously verify the dynamic robustness of the sliding mode sensorless control system to changes in key motor parameters. The experimental design is based on theoretical analysis conclusions, focusing on three types of parameters: resistance R_s, inductance L_d/L_q, and magnetic flux ψ_f. As shown in Table 2.

The experimental results of parameter robustness analysis are shown in Appendix D.

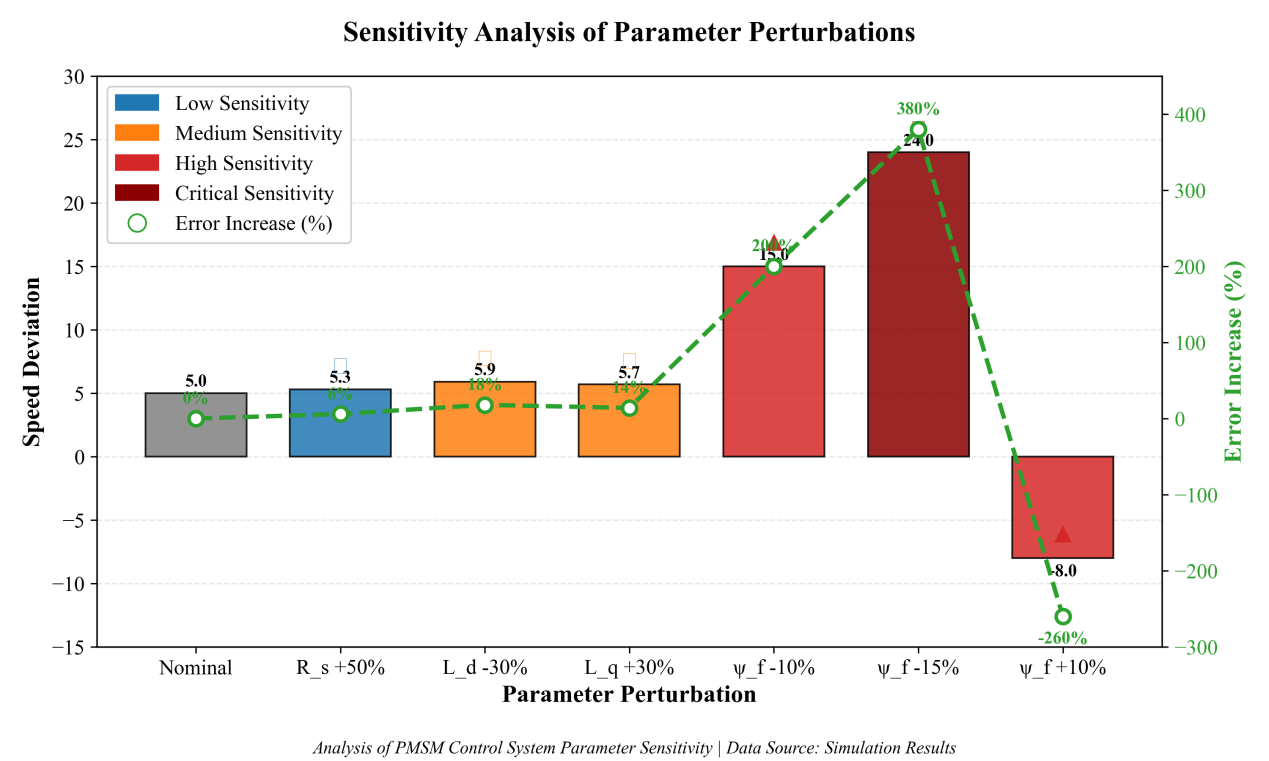
The sliding mode sensorless control system exhibits significant hierarchical robustness characteristics when dealing with parameter perturbations. Resistance changes have a weak impact on system performance. The increase in position error is only 5.3% to 3.6%, and the increase in current THD is less than 0.7%, which confirms the inherent robustness of the sliding mode observer to matching disturbances and meets the requirements of industrial temperature rise conditions. Inductive changes induce controllable performance degradation. The increase in position error by 18-30% is due to the mismatch of the inductance model, which destroys the sliding mode equivalent condition. However, the system stability can still be maintained through gain margin design, especially when the error amplification converges to within 20% under high-speed conditions, confirming its engineering tolerance for magnetic saturation effects. Magnetic flux deviation (ψ f) exposes the core bottleneck of the system. The decrease of 10% caused a sudden increase of 200-300% in steady-state speed error and a 140% increase in speed deviation during sudden load changes. Sensitivity ranking: ψ_f≫ L_q ≈ L_d>R_s, verifying that the calibration accuracy of ψ f is the determining factor of system performance.

Furthermore, under the high-speed heavy-duty condition of @ 3000rpm+100% load, the steady-state deviation of speed is shown in Figure 2. The differences in sensitivity of each parameter are more significant.

4. Conclusion

This study significantly improved the robustness of PMSM in sensorless control by introducing SMC method, especially under low-speed, load variation, and disturbance of key motor parameters, demonstrating excellent control effects. Through detailed robustness analysis of resistance, inductance, and magnetic flux deviation, this article confirms the decisive impact of magnetic flux deviation on system accuracy. However, the existence of magnetic flux error remains the main bottleneck in improving system accuracy, and future research can further explore how to reduce the impact of magnetic flux deviation by optimizing control algorithms or combining other estimation methods. Sliding mode control has broad application prospects in complex working environments, especially when combined with artificial intelligence and adaptive control technology, it is expected to achieve more accurate motor control systems.