Volume 43

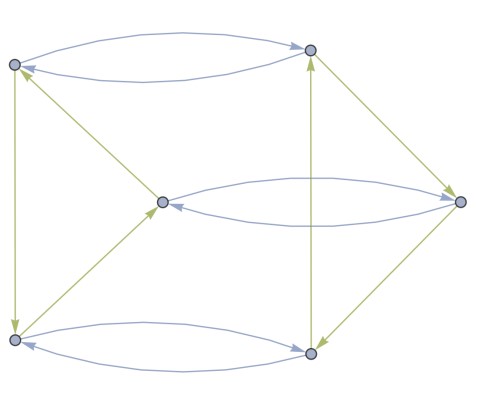
Groups are algebraic structures in Abstract Algebra comprised of a set of elements with a binary operation that satisfies closure, associativity, identity and invertibility. Cayley graphs serve as a visualization tool for groups, as they are capable of illustrating certain structures and properties of groups geometrically. In particular, each element in a group is assigned to a vertex in Cayley graphs. By the group action of left-multiplication, distinct elements in the generating sets can act on each element to create varied directed edges (Meier[1]). By contrast, the presence of a Hamiltonian cycles within a graph demonstrates its level of connectivity. In this research paper, utilizing directed Cayley graphs, we present a series of conjectures and theorems regarding the number and existence of Hamiltonian cycles within Dihedral groups, Symmetric groups of Platonic solids and Symmetric groups. By exploring the relationship between Abstract groups and Hamiltonian graphs, this work contributes to the broader field of research pertaining to Groups of Symmetry and Geometric Group Theory.

Show more

This study employs data from the TESS satellite to investigate the properties of stars. TESS, the Transiting Exoplanet Survey Satellite, offers insights into star activity, periodic variations, and planetary transits by monitoring changes in stellar brightness. Our analysis of TESS data explores critical star attributes, including mass, luminosity, activity levels, and dynamic changes. By examining the relationship between these stellar properties and the presence of planets, we aim to uncover the intricate interplay between celestial bodies and unveil the universe's mysteries. This research encompasses data collection methods, processing techniques, and data analysis approaches, addressing star classifications, parameters, and periodic stellar activity. We also delve into flare energy, which reveals the energy released during stellar flares, and photoperiodic analysis, a tool for understanding periodic light changes in celestial bodies. The study concludes by highlighting the significance of newly discovered planets and the diversity of stars observed by TESS. It underscores the importance of comprehending the connections between stars and planets, shaping our understanding of celestial habitability. In summary, this study enriches our knowledge of star and planet properties, contributing to a broader comprehension of the universe. Through our analysis, we seek to illuminate the complex relationships between celestial entities and unveil the universe's enigmas.

Show more

By analyzing the data of the earth and the sun, we get some of the factors of a planet’s habitability, such as the distance from the star to the planet, the atmosphere, and the tidal locked effect. We use the equation of radiative equilibrium and get the orbital semi-major axis in terms of the star’s radius and the planet’s temperature and albedo. Then, according to the data of the planet and the definition of habitat zone, we can get the range of the habitat zone. We find that the relationship between the radius of the star and the planet’s radius is the radius of the star’s surface, the temperature of the planet’s surface, and the albedo. We also discussed how the albedo, the star mass, the composition of the atmosphere, and the tidal lock influence the planet’s habitability. In conclusion, the only factor of the habitability of a planet is not the distance from the sun to the planet, we need to consider more factors and re-examine the habitability of the planets.

Show more

This paper will analyze different properties of a nuclear collision and their correlation with the geometry of collision using the Glauber Monte-Carlo based calculations. Among all properties, the eccentricity is the main focus of this research. In order to investigate its impact on collision parameters, three-dimensional histograms are created, using given collision parameters, under different categories of numbers of participant nucleons. Comparisons between the histograms allow the exploration of connections between this property and the geometries of lead nuclear collisions, namely, the ellipticity of the collision of the two lead nuclei as eccentricity increases from 0 to 1. Our result is intuitive. The ellipticity of the collision has a positive correlation with the eccentricity, as when the difference between the number of participant nucleons on the L1 and L2 axes increases with eccentricity. The number of nucleons participating in the collision also increases with eccentricity. These are all coherent with past studies conducted in this field.

Show more

The Fourier transform was proposed by Fourier in 1807. Fourier transform is a method of analyzing signals, which can analyze the components of the signal or synthesize the signal using these components. Many waveforms can be used as signal components, such as sine waves, square waves, sawtooth waves, etc. The Fourier transform uses sine waves as components of the signal. Due to its excellent properties, the Fourier transform has a wide range of applications in physics, number theory, combinatorial mathematics, signal processing, probability, statistics, cryptography, acoustics, optics, and other fields. This paper focuses on the study of fractional-order Fourier transform in the engineering field, for the equipment of the tiny fault diagnosis method, and according to some existing diagnostic methods, put forward the idea of diagnostic method enhancement.

Show more

The stock market is volatile, and the prices of stocks are often influenced by various factors that enhance the complexity of stock prediction. According to the literature review, The ARIMA (autoregression average integrated moving average) model is one of the most-used methods for financial prediction, the effectiveness of which has been tested in many countries, which also leads to a need for accurate examination of the model for China’s A-share market. In the paper, Due to its suitability for short-term forecasting, the ARIMA model is utilized to forecast the prices of three representative A-share stocks over 24 days. Finally, the efficiency of the short-term prediction and the low accuracy of the long-term prediction of the ARIMA model are primarily confirmed, which is worthy of further study.

Show more

This paper aims to investigate the influence of stellar winds on the atmosphere of exoplanets. Stellar winds, which consist of charged particles produced by stars, can heavily alter and affect the evolution and composition of exoplanet atmospheres. This paper will provide an overview of stellar wind characteristics and their interactions with exoplanets. It will also investigate the consequences of such interactions, such as atmospheric erosion, atmospheric escape, and the exoplanet’s habitability. In order to develop a more sophisticated and accurate method for identifying habitable planets that may host life, it is necessary to better understand the mechanisms of stellar wind to build more accurate models of stellar wind.

Show more

In the contemporary field of physics, the Higgs boson and the Higgs mechanism stand as captivating subjects of research due to their transformative impact on our comprehension of fundamental particle physics. Their discovery not only bridged a significant gap within the Standard Model but also profoundly influenced our understanding of the evolutionary dynamics of the universe. This paper aims to delve deeply into the Higgs boson and its corresponding Higgs mechanism, thereby furnishing further insights into unraveling the enigma of the cosmos. In the subsequent sections, we will meticulously explore the theoretical underpinnings, experimental observations, and relevant research advancements concerning the Higgs boson and the Higgs mechanism. Through this comprehensive investigation, we aspire to enhance our grasp of the fundamentals of particle physics and the mysteries that enshroud the universe.

Show more

Understanding the development and evolution of the Sun is critical for understanding the origins of our solar system and the circumstances for life on Earth. We can learn about our sun’s dynamics, energy output, and magnetic activity by analysing its evolution, and we can even forecast solar events that affect our world. Extensive study has indicated that the Sun is now in its main sequence stage, but research on its future development, such as becoming a red giant or crashing into a white dwarf, is still underway. Solar evolution research also sheds light on the inner workings of other stars and fundamental processes in the cosmos. The Hertzsprung-Russell diagram aids in the classification and understanding of stars by providing essential information about their life cycle and attributes. The pre-main sequence, main sequence, and post-main sequence stages of the Sun’s origin and development are discussed in this article. It examines the origin of the Sun from interstellar materials as well as the probable impact of core-collapse supernovae. It also delves into the main sequence period, where stars’ masses and ages play important roles in shaping their properties. The main sequence’s existence is linked to hydrostatic equilibrium and the balance of energy production and gas weight. The scattering of stars that depart from the main sequence, such as red giants and white dwarfs, is also discussed in the article. Finally, it dives into post-main sequence development, in which the Sun switches from hydrogen fusion to helium fusion, causing the star to expand and cool. Finally, the Sun’s ultimate phase of development involves the burning of hydrogen and helium, which results in the expulsion of outer layers and the creation of a planetary nebula. The remaining core cools and transforms into a black dwarf, bereft of nuclear and gravitational energy sources.

Show more

Multivariate function calculus is an important part of mathematical analysis courses, and most conclusions can be found and generalized in univariate calculus. However, the biggest difficulty in teaching multivariate calculus lies in its abstraction, such as Taylor’s theorem, multiple integral regions drawing, and integral variable transformation. At the same time, ordinary differential equations are also one of the basic courses of the profession, and dynamic systems based on ordinary differential equations have extensive applications in mathematical models of continuity problems and optimal control problems. Software such as Mathematica, Python, Matlab, etc. can solve similar problems. Therefore, this article will use the visualization and computational capabilities of Mathematica to validate important definitions and conclusions in multivariate calculus, and compare the differences among the three software in solving approximate numerical solutions of dynamic systems of ordinary differential equations from different perspectives.

Show more